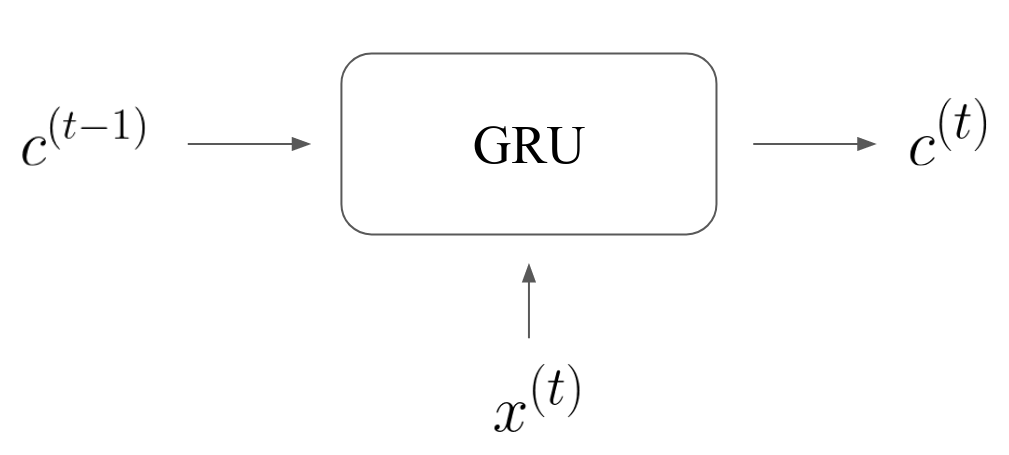
The GRU unit (gated recurrent unit) #1 at time \(\; t \;\) takes as input the previous context vector \(\; c^{(t-1)} \;\) and the current input \(\; x^{(t)} \;\). As output, it gives the current context vector \(\; c^{(t)} \;\).

It works as follows. Using the previous context vector and the current input, it computes a candidate context vector \(\; \tilde{c}^{(t)} \;\) with the potential to replace \(\; c^{(t-1)} \;\) and become the new context vector. The decision of whether to replace \(\; c^{(t-1)} \;\) by \(\; \tilde{c}^{(t)} \;\) or not is done element by element, with a gate function \(\; \Gamma \;\) of the same shape as the context vector, and which ranges between 0 and 1.
All the relevant computations in the GRU have the same form: concatenation of the previous context vector \(\; c^{(t-1)} \;\) and the current input \(\; x^{(t)} \;\), linear transformation and passing through non-linearity (sigmoid for the gates, which needs to be in \(\; [0,1] \;\), or hyperbolic tangent for the candidate context vector, which needs to be more flexible).
\[ g\left(W \left[c^{(t-1)}, x^{(t)}\right] + b \right) \]The first step is computing the candidate context vector \(\; \tilde{c}^{(t)} \;\). As explained, the input is a concatenation of the previous context vector \(\; c^{(t-1)} \;\) and the current input \(\; x^{(t)} \;\). However, we want the candidate \(\; \tilde{c}^{(t)} \;\) to be able to be completely independent from \(\; c^{(t-1)} \;\) if need be. Therefore, we want to be able to blank out elements of \(\; c^{(t-1)} \;\) in the computation of \(\; \tilde{c}^{(t)} \;\). This is done with a first gate, the relevance gate \(\; \Gamma_r \;\).
\begin{align} \Gamma_r &= \sigma\left( W_r \left[ c^{(t-1)}, x^{t} \right] + b_r \right)\\[10pt] \tilde{c}^{(t)} &= \text{tanh}\left( W_c \left[ \Gamma_r \odot c^{(t-1)}, x^{(t)} \right] + b_c \right) \end{align}where \(\; \odot \;\) indicates element-wise multiplication (remember that the gate acts separately on each element).
Once the candidate vector is computed, the context vector is partially updated with it. The decision of whether to update each individual element of the context vector and by how much is made by the update gate \(\; \Gamma_u \;\), which is computed the same as the previous one:
\[ \Gamma_u = \sigma\left( W_u \left[ c^{(t-1)}, x^{(t)} \right] \right) \]And now we can use the gate to combine \(\; c^{(t-1)} \;\) and \(\; \tilde{c}^{(t)} \;\):
\[ c^{(t)} = \Gamma_u \odot \tilde{c}^{(t)} + (1 - \Gamma_u) \odot c^{(t-1)} \]1 Cho et al 2014. On the Properties of Neural Machine Translation: Encoder-Decoder Approaches.